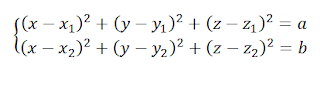This model is an example as application one of
theorems mentioned in article of “The Change Depends on the Direction of the
Motion: The Symmetric Group Action (2)” posted on link:
Work Done by
Force
When we are speaking about the work
done by a force, we have usually two options:
1. The work done on a particle by a
constant force in magnitude and direction which is calculated by below
equation:
2. The work done on a particle by a
varying force in magnitude and direction in which we should use the line
integral to calculate it as follows:
But, in this article, I am willing
to introduce you a special force which has the constant magnitude but varying in
direction. In this case, I have made a model that it is able to show us the
location of the particle after being displaced by this special force.
Suppose a particle P (0, 0, 0) just
like below figure being displaced by a force F:
Theorem: The force with below vector has the constant magnitude equal to 1.22474487139159
but varying in direction:
In this case, we can still use option (1) and below equation
to calculate the work done:
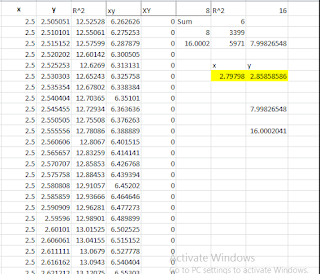
Below figure shows the components of
this model:
Let me explain you about the
components of above model as follows:
1. In left side on
cells C2:D3, we have inputs including the angle φ (degree) of force vector and
amount of displacement of particle “P” which is “r”.
2. In right side on cells F3:J8, we
have outputs including:
2-1) on cells G3:I3, a special force vector can be calculated by using
above theorem.
2-2) on
cells G4:I4, the direction of special force can be obtained by using below
formula:
The magnitude of this force is the
constant and equal to 1.22474487139159.
2-3) on cell G5, we have the work done which
is calculated by below formulas:
2-4) on cells G7:I7, we have the location
particle P (x, y, z) which is derived by this model.
2-5) on cells G8:I8, the direction of motion particle P can be
calculated by using below formula:
2-6) The change of direction particle P will
be done by click on cell A1 and also this change will again go back by click on
cell B1 (Go & Back).
You can see
below screenshot as the examples for this model:
All researchers
and individual people, who are interested in having this model, don’t hesitate
to send their request to below addresses: