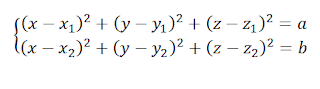The Distances among The Particles in The Space (1)

In physics and engineering, the distances among the particles is usually an important factor for analysis of the subject especially when we are studying Newton’s law of universal gravitation in mechanic, Coulomb’s law in electricity, Maxwell’s equations in electromagnetic theory and so on. But, do you think that the application of the theorems in related to the distances among the particles is limited to above laws in classic physics? Definitely no. The most crucial thing is to predict a flexible system which is moving. For instance, suppose you have a bowl filled by water in your hand. When you move, how can you predict the motion of water system into the bowl? Of course, when we are speaking about a rigid system, the prediction and analysis of this system is easy just like when you are moving by a car (an approximately rigid system).

In the reference with article of “A Specific Permutation And Applications”, we can derive many conjectures (or theorems) or properties in related to the distances among the particles in the space. Consequently, this could be conducted as a big project in which I will not be able to handle this project alone.

 In this series, I will post little by little these new properties accompanied by examples only related to Newton's law of universal gravitation in mechanic. Since I am using the big data analysis to extract these properties, I have not any pure mathematics proof for them. Therefore, I will mark up them as the Conjectures instead of the Theorems. As the matter of fact, this is the Big Data Analysis with Microsoft excel to create the value from data.

Conjecture (1):

If above article (A Specific Permutation…) has been applied for only three choices from many events (sample space), we will have the concentric spheres or layered spheres just like below figure:

In previous article, I told you a specific permutation with n = 6 and r =3, gives us 48 points on a sphere, If we increase the sample space (n) to 8 and r = 3, we will have 4 concentric spheres which gives us 48 points on each sphere and for n = 10, we will have 10 concentric spheres which gives us 48 points on each sphere and for n = 12, we will have 20 concentric spheres which gives us 48 points on each sphere and etc..

In fact, the number of the layered spheres can be calculated by using previous equation divided to 

48.

Note: I will again comeback to this conjecture as soon as possible.

Conjecture (2):

The distance of each point on a sphere is equal to at least five pair points on the same sphere.

Suppose points P1, P2, P3, P4, P5, P6, P7, P8, P9, P10, P11 have been located on a sphere. This conjecture says to us:

d (P1, P2) = d (P1, P3)  = A

d (P1, P4) = d (P1, P5)  = B

d (P1, P6) = d (P1, P7)  = C

d (P1, P8) = d (P1, P9)  = D

d (P1, P10) = d (P1, P11)  = E

Where:  

d (P1, P2) = the distance between point P1 to P2

The amounts of A, B, C, D, E are the members of real number

Note: I will again comeback to this conjecture as soon as possible.

Conjecture (3):

The distances among the points P1(x, y, z), P2 (z, x, y) and P3(y, z, x) are always the same.

d (P1, P2) = d (P1, P3) = d (P2, P3)

Example:

Suppose point P1 has below coordination:

P1 (3, -5, 11)

Therefore, the coordination P1 and P2 will be:

P2 (11, 3, -5)

P3 (-5, 11, 3)

d (P1, P2) = d (P1, P3) = d (P2, P3) = 19.59592

Let me tell you an example about Newton’s law of universal gravitation as follows:

The Mapping A System of Three Particles for Given Gravity Potential Energy And The Distance

Suppose we have three particles P1, P2 and P3 with the distances among them in infinity   which have the masses of m1, m2 and m3. If an external force brings all these particles in new location just like below figure, how can we calculate total work done on them?

It is clear; the work done on particles is equal to total gravity potential energy of system but in opposite direction in which we can write below equation for total gravity potential energy of system:

Where:

G = Gravitational constant = 6.672E-11   (N.m2/kg2)

U (r) = total gravity potential energy of system   (J)

r = the distance among the particles   (m)

m1, m2,m3 = mass (kg)

Question (1):

If we have:

U (r) = -0.04143312 J

r = 0.0002 m

How can we map these particles in the space?

Step (1):

To find masses of particles, we should apply the method mentioned in article of “Solving a Nonlinear Equation with Many Independent Variables”

I found 6 answers for mass of the particles:

m1	m2	m3
6	300	400
6	400	300
15	380	300
22	100	1000
40	130	700
40	330	300

Step (2):

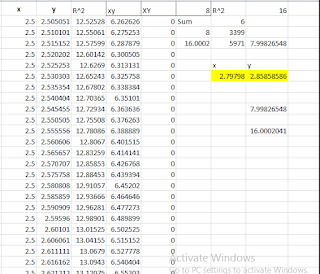
Since the distance is equal to 0.0002 m, we can find the coordination of particle P1 by using the model presented in article of “A Model to Track the Location of a Particle in the Space” 

I found 408 answers for coordination of particle P1 as follows:

Here I have posted some of the results:

Models	x	y	z
1	-0.0005	-0.00047	-0.00035
2	-0.0005	-0.00037	-0.00035
3	-0.0005	-0.00035	-0.00047
4	-0.0005	-0.00035	-0.00037
5	-0.00047	-0.0005	-0.00035
6	-0.00047	-0.00045	-0.00032
7	-0.00047	-0.00035	-0.0005
8	-0.00047	-0.00035	-0.00032
9	-0.00047	-0.00032	-0.00045
10	-0.00047	-0.00032	-0.00035
11	-0.00045	-0.00047	-0.00032
12	-0.00045	-0.00042	-0.00029
13	-0.00045	-0.00032	-0.00047

14	-0.00045	-0.00032	-0.00029
15	-0.00045	-0.00029	-0.00042
16	-0.00045	-0.00029	-0.00032
17	-0.00042	-0.00045	-0.00029
18	-0.00042	-0.0004	-0.00027
19	-0.00042	-0.00029	-0.00045
20	-0.00042	-0.00029	-0.00027
21	-0.00042	-0.00027	-0.0004
22	-0.00042	-0.00027	-0.00029
23	-0.0004	-0.00042	-0.00027
24	-0.0004	-0.00037	-0.00024
25	-0.0004	-0.00027	-0.00042
26	-0.0004	-0.00027	-0.00024
27	-0.0004	-0.00024	-0.00037
28	-0.0004	-0.00024	-0.00027
29	-0.00037	-0.0005	-0.00035
30	-0.00037	-0.0004	-0.00024
31	-0.00037	-0.00035	-0.0005
32	-0.00037	-0.00035	-0.00022
33	-0.00037	-0.00024	-0.0004
34	-0.00037	-0.00024	-0.00022
35	-0.00037	-0.00022	-0.00035
36	-0.00037	-0.00022	-0.00024
37	-0.00035	-0.0005	-0.00047
38	-0.00035	-0.0005	-0.00037
39	-0.00035	-0.00047	-0.0005
40	-0.00035	-0.00047	-0.00032
41	-0.00035	-0.00037	-0.0005
42	-0.00035	-0.00037	-0.00022
43	-0.00035	-0.00032	-0.00047
44	-0.00035	-0.00032	-0.00019
45	-0.00035	-0.00022	-0.00037
46	-0.00035	-0.00022	-0.00019
47	-0.00035	-0.00019	-0.00032
48	-0.00035	-0.00019	-0.00022
49	-0.00032	-0.00047	-0.00045
50	-0.00032	-0.00047	-0.00035
51	-0.00032	-0.00045	-0.00047
52	-0.00032	-0.00045	-0.00029
53	-0.00032	-0.00035	-0.00047
54	-0.00032	-0.00035	-0.00019
55	-0.00032	-0.00029	-0.00045
56	-0.00032	-0.00029	-0.00017
57	-0.00032	-0.00019	-0.00035
58	-0.00032	-0.00019	-0.00017

Please be informed that each answer gives us a model of three particles P1, P2 and P3. For instance, look at Model (1) in above table. By applying the conjecture (3), you can find below system of articles:

	x	y	z	Distance
P1	-0.0005	-0.00047	-0.00035	0.00020
P2	-0.00035	-0.0005	-0.00047	0.00020
P3	-0.00047	-0.00035	-0.0005	0.00020

As you can see, the distance among P1, P2 and P3 is equal to 0.0002 m.

Now, please comeback to step (1), we have 6 answers for the masses and for each answer of masses, we have 408 models. It means that we found 2448 systems of three particles which have the same total gravity potential energy.

Question (2):

If we have:

U (r) = -0.01748064 J

r = 0.0002 m

How can we map these particles in the space?

It is clear, the number of models is 408 but the answers of masses are as follows:

m1	m2	m3
4	100	500
10	240	200
20	20	1300
20	220	200
30	380	100
31	200	200
40	60	500

It means that we found 2856 systems of three particles which have the same total gravity potential energy.

Question (3):

If we have:

U (r) = -2.27021E-06 J

r = 1.54 m

How can we map these particles in the space?

The answers for masses are just like to question (2):

m1	m2	m3
4	100	500
10	240	200
20	20	1300
20	220	200
30	380	100
31	200	200
40	60	500

But the answers for step (2) are as follows:

Models	x	y	z
1	-0.31	0.09	0.923333
2	-0.31	0.523333	0.923333
3	-0.31	0.923333	0.09
4	-0.31	0.923333	0.523333
5	-0.27667	0.123333	0.956667
6	-0.27667	0.556667	0.956667
7	-0.27667	0.956667	0.123333
8	-0.27667	0.956667	0.556667
9	-0.24333	0.156667	0.99
10	-0.24333	0.59	0.99
11	-0.24333	0.99	0.156667
12	-0.24333	0.99	0.59
13	0.09	-0.31	0.923333
14	0.09	0.923333	-0.31
15	0.123333	-0.27667	0.956667
16	0.123333	0.956667	-0.27667
17	0.156667	-0.24333	0.99
18	0.156667	0.99	-0.24333
19	0.523333	-0.31	0.923333
20	0.523333	0.923333	-0.31
21	0.556667	-0.27667	0.956667
22	0.556667	0.956667	-0.27667
23	0.59	-0.24333	0.99
24	0.59	0.99	-0.24333
25	0.923333	-0.31	0.09
26	0.923333	-0.31	0.523333
27	0.923333	0.09	-0.31
28	0.923333	0.523333	-0.31
29	0.956667	-0.27667	0.123333

30	0.956667	-0.27667	0.556667
31	0.956667	0.123333	-0.27667
32	0.956667	0.556667	-0.27667
33	0.99	-0.24333	0.156667
34	0.99	-0.24333	0.59
35	0.99	0.156667	-0.24333
36	0.99	0.59	-0.24333

In fact, we can find 252 systems of three particles which have the same total gravity potential energy.

As you can see, when the distances increase, the work done on systems will decrease.

A Model for Making Two Ways Stochastic Matrix

Making a two ways stochastic matrix can be very hard especially when you have many elements in matrix such as a matrix 5*5 or 6*6 and more. But, what is two ways stochastic matrix? A two ways stochastic matrix is when the sum of all elements on each column and row are equal to 1. What is the application of the two ways stochastic matrix? In the reference with article of “Does this conjecture lead us toward an absolute justice in the world?” posted on link: http://www.emfps.org/2018/02/a-model-to-produce-magic-matrix.html, by using a two ways stochastic matrix, we will be able to predict a subject by using the Markov process.

Suppose company X has a delivery system, if this company wants to use the Markov chain to forecast the probability of delivery on each station, it will have to investigate the statistics during the period of a specific time to obtain many probability numbers.

Assume, the company has 5 stations and according to its statistics, it has gotten 10 probabilities. There are two questions:

1. Can these 10 probabilities make a two ways stochastic matrix?

2. If the answer to question (1) is positive, what is two ways stochastic matrix?

Below model is able to answer above questions:

Let me explain you about the components of above model as follows:

1. On cells P3:Y3, we have inputs including 10 probability

2. On cells Q4:T4, there are the errors. The error on the sum of rows is error.H and the error on the sum of columns is error.V.

3. On cells Q6:U10, we have outputs which give us a two ways stochastic matrix.

You can see below captured movie as the example for this model:

All researchers and individual people, who are interested in having this model, don’t hesitate to send their request to below addresses:

https://t.me/Allisnumber

A Specific Permutation And Applications (1)

The base of the probability theory is always referred to permutations and combinations in which a permutation is an ordered combination. It means, if we have “n” events and choose “r” of them, we will have the opportunity to make many groups and subsets which are “r” from “n” where the repetition and the replacement will also give us new concepts.

As you know, basically we have two types of permutations:

1.      Permutations with repetition which is calculated by below formula:

The number of Permutations = n^r

2.      Permutations without repetition which is obtained by below formula:

            The number of Permutations = n!/(n-r)!

The purpose of this article is to introduce a specific permutation.

A specific permutation

Suppose we have a number of events “n” and we consider whole events as the pairs just like below set:

S = {(a1,a2), (b1,b2), (c1,c2), (d1,d2)….}

Here "S" is our sample space.
We are willing to make all permutations without repetition with “r” members from “S” where each set of permutations is included only one of the pairs. This is additional restriction for these permutations. It is clear; “r” must be always smaller or equal half of “n”.

Therefore, the characteristics of this specific permutation are defined as follows:

·        n = 2k   and   k ε N

·        r ≤ n/2

·        Each set of permutations is included only one of the pairs

The question is:  How can we calculate the number of these permutations?

By using below formula, we will be able to get the number of all permutations:

For instance, when we choose three choices from six events, we will have 48 permutations or if we have three choices from eight events, we will get 192 permutations.

By using Microsoft excel, we can generate all permutations on a spreadsheet of excel.

Example: Generating the Points on a Sphere

Suppose our sample space or events are pairs of plus and minus as follows:

S = {(-a, a), (-b, b), (-c, c)…}

In this case, for n = 6 we will have: 48 points which have been located on a sphere.

Assume we have the point P (2, 5, 24) in the 3D space in which the sample space will be below cited:

S = {(-2, 2), (-5, 5), (-24, 24)}

All below points are located on a sphere or gives us a field in 3D space:

Below model gives us all 48 points on a sphere when we have only coordination of one point:

In above model, the inputs are the coordination of one point P (x,y,z) and the outputs are the coordination of all 48 points on a sphere. As you can see, the radius of sphere (r) always stays the constant.

In the reference with above mentioned, below movie as well as shows an overall shape of this system when the location of a point is changed:

Does this conjecture lead us toward an absolute justice in the world?

Eigenvalue equal to the sum of all elements on each column or row

One of the properties two ways matrices which can be easily proved is, to obtain the Eigenvalue where the sum of all elements on each column or row is equal to Eigenvalue of these matrices.

Another interesting property of a two way matrix is, to have a special eigenvector that all elements of it are the same. It means, if “M” is a two ways matrix, vector “V” will be eigenvector of matrix “M” where we have:

V = (x, x, x, x, ….)  and    λ = the sum of all elements on each column or row

This property can be easily proved. 

Following to article of “The Impact of Stochastic Matrix on Any Vector”, let me tell you about another conjecture as follows:

Conjecture (2): The final result of Markov Process including the impact of a two ways stochastic matrix on any vector will be a vector with the same elements where each element will be equal to average all elements of initial vector.

Initial Vector: V0 = (a, b, c, d,….) and M = two ways stochastic matrix

Example:

Does this conjecture lead us toward an absolute justice in the world?

A Model for Analysis of Work Done by a Special Force

This model is an example as application one of theorems mentioned in article of “The Change Depends on the Direction of the Motion: The Symmetric Group Action (2)” posted on link:

http://www.emfps.org/2017/08/the-change-depends-on-direction-of_9.html?m=1

Work Done by Force

When we are speaking about the work done by a force, we have usually two options:

1. The work done on a particle by a constant force in magnitude and direction which is calculated by below equation:

2. The work done on a particle by a varying force in magnitude and direction in which we should use the line integral to calculate it as follows:

But, in this article, I am willing to introduce you a special force which has the constant magnitude but varying in direction. In this case, I have made a model that it is able to show us the location of the particle after being displaced by this special force.

Suppose a particle P (0, 0, 0) just like below figure being displaced by a force F:

Theorem: The force with below vector has the constant magnitude equal to 1.22474487139159 but varying in direction:

In this case, we can still use option (1) and below equation to calculate the work done:

Below figure shows the components of this model:

Let me explain you about the components of above model as follows:

1. In left side on cells C2:D3, we have inputs including the angle φ (degree) of force vector and amount of displacement of particle “P” which is “r”.

2. In right side on cells F3:J8, we have outputs including:

   2-1) on cells G3:I3, a special force vector can be calculated by using above theorem.

   2-2) on cells G4:I4, the direction of special force can be obtained by using below formula:

The magnitude of this force is the constant and equal to 1.22474487139159.

 2-3) on cell G5, we have the work done which is calculated by below formulas:

  2-4) on cells G7:I7, we have the location particle P (x, y, z) which is derived by this model.

  2-5) on cells G8:I8, the direction of motion particle P can be calculated by using below formula:

 2-6) The change of direction particle P will be done by click on cell A1 and also this change will again go back by click on cell B1 (Go & Back).  

You can see below screenshot as the examples for this model:

All researchers and individual people, who are interested in having this model, don’t hesitate to send their request to below addresses:

https://t.me/Allisnumber

A Model to Solve a System of Nonlinear Equations by Using Microsoft Excel

This is an example for solving a system of nonlinear equations by using the Big Data Science Analysis with Microsoft excel plus VBA.

Definitely, there are many complicated problems that can be solved by using this analytic model. For instance, one of the applications of this model is to solve problems related to optimization, such as Hill Climbing.

For example, what is the maximum area of a rectangle inscribed in a circle with a radius of 2 units?

You can find the answers for “x” and “y” in this rectangle in the below data analysis:

I would like to inform you that this model is able to solve all linear and nonlinear system of equations in which it gives us less error than traditional methods such as Newton – Raphson , Gauss – Seidel, Jacobian and so on. Don't worry, if you have not any knowledge about traditional methods. Dive into new technology.

Example: A Model to Track the Location of a Particle in the Space

 One of the most important needs for many projects is, quickly to track the motion of a particle when

it is tripping between two points in the space. For instance, suppose particle P is moving by velocity “V” with accelerate equal to zero from point A (x1, y1, z1) to point B (x2, y2, z2). We want to know the coordination of P (x, y, z) at the moment of “t” when it is moving in direction of A to B. This model gives us the opportunity to obtain the coordination P (x, y, z) only by click. In fact, if we have the coordination P (x, y, z), it will be as an index for us that other particles which are moving from A to B such as P1, P2, …. are not tripping in the exact direction of A to B. In this case, we have to solve a system of two nonlinear equations as follows:

 First of all, we should define amount of “a” and “b” as follows:

The distance of point A to point B is calculated by using below formula and also “X” is the distance that particle P will travel after time “t” in direction of A to B:

Therefore, we should solve below system of two nonlinear equations

Below figure as well as shows you the components of this model

Let me explain you about the components of above model as follows:

1. In right side on cells G4:J10, we have inputs including the coordination points A and B, velocity of particle P (v), the time after staring to travel particle P (t) and Error which is the difference between the results. So, X = v.t, d = distance between point A and B and on cell G10, I have included a logic formula (=if (H8 >= H9, H8, 0)). It means, if X = 0 then the particle has passed point B

2. In left side on cells C5:E6, we have other inputs including the ranges to reach to the answer for coordination particle P (x, y, z) which is the solution for system of two nonlinear equations. 
 Here, there are lower and upper ranges which are changed by click on cell A2 and also this change will again go back by click on cell B2 (Go & Back).

This part has been utilized by the method stated in article of “Can We Solve a Nonlinear Equation with Many Variables?” posted on link:
http://emfps.org/2016/10/can-we-solve-nonlinear-equation-with.html 

3. On cells C9:E9, we have outputs which are the answer to above 

system of two nonlinear equations.

4. On cells C12:E13, we have Control (1) where first equation is solved by using the coordination A 

and P and it is compared with amount of “X^2” on cell C14. So, second equation is solved by using the coordination B and P and it is also compared with amount of “(d-X)^2”on cell C15. The differences have been mentioned on cell G12 and G13 as the errors.

5. On cells E15:G17, we have Control (2) which is referred to track the directions in which we are willing to know if the motion of particle P is in direction from point A to point B. In this case, a control can be conducted by using below formulas:

You can see below screenshot as the examples for this model:

Conclusion

.Above article gives you a simple example

In fact, I am willing to tell you that this model is able to solve all system of two or three nonlinear   

equations.

All researchers and individual people, who are interested in having this model, don’t hesitate to send 
their request to below addresses:

https://t.me/Allisnumber